قضیه شکاف جانبی -کلاس یار

این محتوا با تلاش تیم کلاس یار جمع آوری و منتشر شده است.

قضیه شکاف ضلعی بیان می کند که اگر خطی موازی یک ضلع مثلث باشد و از دو ضلع دیگر عبور کند، آن گاه آن اضلاع را به نسبت تقسیم می کند. به شکل زیر نگاه کنید.

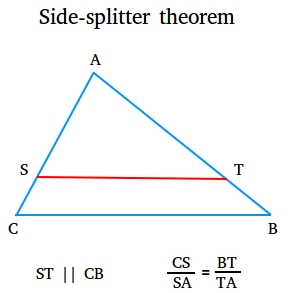
از آنجایی که ST موازی با CB است، پس CS / SA = BT / TA است

توجه داشته باشید که ST خط وسط مثلث نیست. به عبارت دیگر، S نقطه وسط CA و T نقطه میانی BA نیست.

استفاده از قضیه شکاف ضلعی برای حل یک مسئله هندسی.

در شکل زیر AB موازی با UT است. اگر UA = 36، TB = 9، و BS = 3، x را پیدا کنید.

از آنجایی که AB با UT موازی است، می‌توانیم از قضیه شکاف جانبی استفاده کنیم.

UA / AS = TB / BS

جایگزین

36 / x = 9 / 3

x را با ضرب متقاطع حل کنید

36 × 3 = x × 9

108 = 9 برابر

دو طرف را بر 9 تقسیم کنید

108/9 = 9x/9

12 = x

از این صفحه لذت می برید؟ لطفا آن را فوروارد پرداخت کنید. در اینجا نحوه …

آیا ترجیح می دهید این صفحه را با پیوند دادن به آن با دیگران به اشتراک بگذارید؟

1. روی کد لینک HTML زیر کلیک کنید.
2. آن را کپی و جایگذاری کنید و یادداشتی از خود اضافه کنید، در وبلاگ، یک صفحه وب، انجمن ها، یک نظر وبلاگ، حساب فیس بوک خود یا هر جایی که برای شخصی این صفحه ارزشمند است.

منبع

لطفا ستاره بده (سمت چپ بیشترین امتیاز)

https://classyar.com/side-splitter-theorem-html/

https://classyar.com
کلاس یار