استاندارد کردن یک توزیع عادی -کلاس یار

این محتوا با تلاش تیم کلاس یار جمع آوری و منتشر شده است.

استاندارد کردن یک توزیع نرمال تبدیل یک توزیع نرمال به توزیع نرمال استاندارد است. در کاربردهای دنیای واقعی، یک متغیر تصادفی پیوسته ممکن است دارای توزیع نرمال با مقدار میانگین متفاوت از 0 و مقدار انحراف استاندارد متفاوت از 1 باشد.

در این مورد، باید توزیع نرمال را استاندارد کنیم تا بتوانیم از جدول توزیع نرمال استاندارد برای یافتن نواحی یا احتمالات زیر منحنی نرمال استفاده کنیم.

واحدهای توزیع نرمال با x و واحدهای توزیع نرمال استاندارد با z نشان داده می شوند.

فرمول مورد استفاده در هنگام استانداردسازی توزیع نرمال، نمرات استاندارد شده است

μ و σ میانگین و انحراف معیار توزیع نرمال x هستند.

مثال شماره 1

فرض کنید x یک متغیر تصادفی پیوسته باشد که معمولاً با میانگین 30 و انحراف معیار 4 توزیع می شود. مساحت بین x = 30 و x = 39 را بیابید.

اولین مرحله استاندارد کردن توزیع نرمال داده شده با تبدیل x = 30 و x = 39 به مقادیر z مربوطه با استفاده از فرمول بالا است.

برای x = 30،

برای x = 39،

مساحت زیر منحنی نرمال بین x = 30 و x = 39 برابر است با مساحت زیر منحنی بین z = 0 و z = 2.25

P(30 < x < 39) = P(0 < z < 2.25)

با استفاده از تکنیک درس مربوط به مساحت زیر منحنی نرمال استاندارد می بینیم که P(0 < z < 2.25) = 0.4878

مثال شماره 2

فرض کنید x یک متغیر تصادفی پیوسته است که معمولاً با میانگین 50 و انحراف معیار 6 توزیع می شود. مساحت بین x = 41 و x = 59 را بیابید.

اولین مرحله استاندارد کردن توزیع نرمال داده شده با تبدیل x = 41 و x = 59 به مقادیر z مربوطه با استفاده از فرمول است.

برای x = 41،

برای x = 59،

مساحت زیر منحنی نرمال بین x = 41 و x = 59 برابر است با مساحت زیر منحنی بین z = -1.5 و z = 1.5

P(41 < x < 59) = P(-1.5 < z < 1.5)

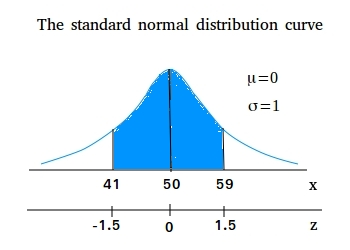
P(-1.5 < z < 1.5) = P(-1.5 < z <0) + P(0 < z < 1.5)

از آنجایی که توزیع نرمال متقارن است، P(-1.5 < z < 0 ) = P(0 < z < 1.5)

با استفاده از جدول توزیع نرمال استاندارد، P(0 < z < 1.5) = 0.4332

P(-1.5 < z < 1.5) = 0.4332 + 0.4332 = 0.8664

از این صفحه لذت می برید؟ لطفا آن را فوروارد پرداخت کنید. در اینجا نحوه …

آیا ترجیح می دهید این صفحه را با پیوند دادن به آن با دیگران به اشتراک بگذارید؟

1. روی کد لینک HTML زیر کلیک کنید.
2. آن را کپی و جایگذاری کنید و یادداشتی از خود اضافه کنید، در وبلاگ، یک صفحه وب، انجمن ها، یک نظر وبلاگ، حساب فیس بوک خود یا هر جایی که برای شخصی این صفحه ارزشمند است.

منبع

لطفا ستاره بده (سمت چپ بیشترین امتیاز)

https://classyar.com/standardizing-a-normal-distribution-html/

https://classyar.com
کلاس یار